
머신러닝에서 딥러닝으로 넘어가며 ‘거리’에 대한 사고가 어떻게 변했는지를 정리한 글입니다. 거리 기반 ML(Machine Learning) 모델링의 한계(XOR 문제 등)를 이해하고, 은닉층과 고차원 표현을 통해 딥러닝이 어떻게 새로운 기준을 학습하는지를 설명합니다. ML 경험자에게 DL(Deep Learning) 개념 전환을 돕는 개념 중심 글입니다.
1. 데이터 분석과 거리 개념의 익숙함
- 데이터 분석과 머신러닝에서는 대부분의 판단 기준이 거리 기반이었다.
- 유클리디안 거리, 코사인 유사도, KNN, 클러스터링 등
- 벡터 간 거리가 작으면 유사, 멀면 이질적이라는 직관
- 이 개념은 “공간 상에 점이 어떻게 퍼져 있는가”를 관찰하고 분류하는 데 탁월하다.
- 필자 역시, EDA나 추천 시스템 등을 설계할 때 ‘거리’를 어떻게 정의하느냐에 많은 시간을 들였다.
2. 머신러닝은 평면에서의 거리 기준을 세운다
- ML 모델은 대부분 사람이 기준을 정하는 구조였다.
- 선형 회귀, SVM, 의사결정트리 등
- 기준선을 정하고, 이 기준선(결정경계)을 기준으로 데이터를 나누는 방식
- 이 과정에서는 ‘거리’가 여전히 의미를 가진다. 기준선까지의 거리, 클러스터 중심과의 거리 등
- 그러나 여기서 한계가 생긴다: 선 하나로 나눌 수 없는 분포는 어떻게 할 것인가?
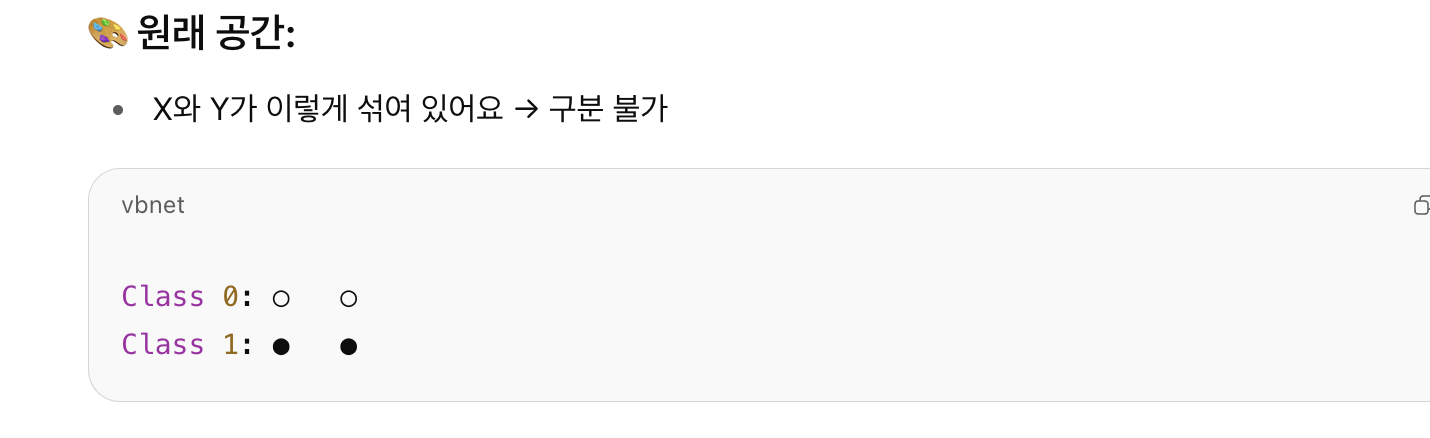
3. XOR 문제, 거리의 실패를 보여주다
- XOR 문제는 대표적인 비선형 문제다.
- (0,0) → 0 / (1,1) → 0 / (1,0), (0,1) → 1
- 이 네 점은 선 하나로는 분리되지 않는다
- ML 방식으로는 어떤 기준선을 그어도 제대로 분류가 되지 않는다.
- 거리 기반 유사성도 무력해진다
- 이 부분에서 꽤 오래 멈춰 있었다. ‘거리 기준으로 분리되지 않으면 어떡하지?’

4. 딥러닝: 공간을 구부려 새로운 기준을 만든다
4.1 선형 분리란 무엇인가: 직선으로 나눌 수 있는 문제
- ‘선형 분리(Linear separability)’란, 데이터를 하나의 직선(또는 초평면)으로 구분할 수 있다는 의미다.
- 예: 붓꽃(Iris) 데이터처럼, 두 클래스가 특정 축(길이, 너비 등)을 기준으로 잘 나뉜다면 이는 선형 분리 가능한 경우다.
- 선형 분리는 계산이 단순하고 해석이 쉬워서, 초기 ML 모델들의 기본 전제가 되었다.
- 하지만 모든 데이터가 선형 분리 가능한 것은 아니다. 이때가 바로 머신러닝의 한계점이다.
4.2 딥러닝은 ‘은닉층’을 통해 문제를 해결한다
- 은닉층은 입력값을 새로운 표현 공간으로 보내는 중간 단계다.
- ReLU 같은 비선형 함수는 입력 공간을 비틀어 평면에서는 분리되지 않던 값을 분리 가능하게 만든다.
- 이 과정을 통해 ‘구부러진 공간’에서 새로운 분리 기준이 만들어진다.


4.3 ML과 다른 점: 기준을 사람이 아닌, 모델이 학습으로 만든다
- ML에서는 사람이 결정경계를 설정했지만, DL에서는 학습을 통해 적절한 기준이 만들어진다.
- 이때 '거리' 역시 학습을 통해 변형되며, 은닉층에서의 표현이 핵심이 된다.
4.4 질문을 따라가며 이해한 은닉층의 작동 방식
- “은닉층으로 옮겨간다는 건, 입력값이 어디론가 이동한다는 건가?”
- “그럼 동일한 출력값을 가진 입력들이 서로 다른 방향으로 이동해도 괜찮은가?”
- “위상이 깨져도 결과만 같으면 되는 건가?”
- 이 질문을 거치며 깨달은 건, 은닉층은 원래 공간을 구부려서 새로운 위상을 만드는 과정이라는 것.
- 종이를 비틀어 못 만나던 점을 만나게 만드는 것처럼, 위상은 바뀌어도 결과 기준은 보존된다는 원리.
4.5 ReLU와 아웃라이어 제거: 표면적 유사성과 본질적 차이
- ReLU는 음수를 0으로 만드는 활성화 함수다. 표면적으로는 ML에서의 아웃라이어 제거와 비슷해 보인다.
- 하지만 ML은 사람이 기준을 정해 제거하는 반면, DL에서는 학습 안정성과 비선형성을 위해 수학적으로 자동 적용된다.
- 즉, 개입의 방식과 목적이 전혀 다르다.
4.6 은닉층, 활성화 함수, 반복 학습이 DL의 본질
- 딥러닝은 기존 기준을 학습으로 대체하고, 은닉층을 통해 구부러진 표현 공간을 만들어낸다.
- 이로써 사람의 기준이 아닌, 문제에 최적화된 기준을 갖게 된다.
5. 왜 이게 중요한가: 사람의 직관과 기계의 학습
- 사람은 눈에 보이는 거리 기반으로 사고한다. 그래서 ML이 직관적으로 와닿는다
- 그러나 현실 문제는 더 복잡하다. 어떤 기준으로도 분리되지 않는 경우가 많다
- DL은 이런 경우, 새로운 표현 공간을 만들어 문제를 푼다. 이게 ‘고차원 표현력’이다
- 단, 이 구조가 잘 작동하려면 충분한 양의, 왜곡되지 않은 데이터가 필요하다
- 실제로 참여했던 프로젝트에서는 EDA와 Athena 샘플링을 통해 데이터 왜곡을 사전에 확인했기 때문에 DL 적용 전에 문제를 감지할 수 있었다
6. 정리하며: 거리 개념은 여전히 유효하지만, 전혀 다른 방식으로
- DL에서도 거리 개념은 여전히 중요하다 (예: 임베딩 벡터 간 거리)
- 다만, 그 거리 자체를 학습으로 만드는 것, 이게 ML과 DL의 본질적 차이다
- 이 차이는 다음과 같은 구조적 전환으로 정리할 수 있다:
- ML: 사람의 기준 → 거리 기반 모델링
- DL: 학습된 기준 → 은닉공간 기반 표현
- 그리고 이 흐름의 연장선에서 LLM(Large Language Model)이 등장했다.
단어 간 의미의 ‘거리’도 학습을 통해 표현되고, 임베딩 공간은 더 이상 고정된 피처맵이 아닌, 문맥과 의미에 따라 동적으로 구부러지는 공간이 되었다.
덧붙임
이 글은 기술적 정답보다는, 개념적 이해의 흐름을 중심으로 정리한 글이다. ML에서 DL로 넘어가며 개념적으로 막힌 사람이라면, ‘거리’라는 단어 하나로 그 차이를 설명해 보는 것도 좋은 방법이 될 수 있다.
'AI, 기술적인 이야기들' 카테고리의 다른 글
| LLM 설계자를 위한 구조적 이해: 벡터 DB는 왜 필요한가 (1) | 2025.06.12 |
|---|---|
| DL에서 LLM으로 ② 붙이는 것과 설계하는 것은 다르다 (0) | 2025.06.11 |
| ChatGPT는 왜 그렇게 'AI처럼' 느껴질까? – AI UX의 착시 현상을 파헤치다 (0) | 2025.06.09 |
| LLM 개념 입문, 질문에서 시작하기 (0) | 2025.06.05 |
| Dense Layer는 왜 필요할까 – GPT가 말처럼 말할 수 있는 구조적 이유 (0) | 2025.06.02 |